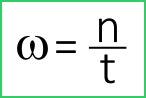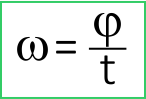Угловая скорость измеряется в

Единицы измерения скорости при вращательном движении

Единицы измерения скорости при поступательном движении

Единицы, часто применяемые в судовой электротехнике

При поступательном движении скорость движущихся масс называется «линейная скорость», обозначается латинской буквой «υ» и измеряется в «м/с» ( метр в секунду ) или «м/мин» ( метр в минуту ).Например, скорость подъёма груза электропривода лебёдки υ = = 30 м/мин.

На практике применяют внесистемные ( не соответствующие системе СИ ) едини-

цы измерения скорости, например, километр в час ( км/ч ), узел = 1852 м /ч ( 1852 м – дли-

на морской мили ) и др.

При измерении скорости вращающихся масс применяют два наименования скоро-

1. «частота вращения», обозначается латинской буквой «n» и измеряется в

«об/мин» ( оборот в минуту ). Например, частота вращения двигателя n = 1500 об/мин.

Эта единица скорости – внесистемная, т.к. в ней используется внесистемная едини

ца времени, а именно – минута ( в системе СИ время измеряется в секундах ).

Тем не менее эта единица до сих пор широко применяется на практике. Например, в паспортных данных электродвигателей скорость вала указывается именно в об/ мин.

2. «угловая скорость», обозначается латинской буквой «ω» и измеряется в

«рад/с» ( радиан в секунду ) или, что одно и то же, с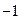( секунда в минус первой степени ).

Например, угловая скорость электродвигателя ω = 157 с.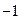

Напомним, что радиан – вторая, кроме знакомого нам пространственного градуса

( º ), единица измерения углового расстояния, равная 360º / 2π = 360 / 2*3,14 = 57º36′ ( пять

десят семь градусов и 36 минут ).

Впервые возникла в расчетах, где часто встречалось число 360º / 2π.

Эта единица скорости – системная, т.к. в ней используется системная единица вре-

мени, а именно – секунда.

На практике надо уметь быстро переходить от одной единицы скорости к другой и наоборот.

Поэтому выведем соотношение между этими двумя единицами.

Угловая скорость ( через частоту вращения ):

ω = 2 πn / 60 = n / ( 60 / 2 π ) = n / 9,55 ≈ n / 10 ( В.1 ).

Частота вращения ( через угловую скорость ):

n = 60 ω / 2 π = 60 ω / 2*3,14 = 9,55 ω ≈ 10 ω ( В.2 ).

Приведем два примера.

В паспорте электродвигателя указана номинальная скорость вала n = 1500 об/мин.

Найти угловую скорость вала этого электродвигателя.

Угловая скорость вала

ω =n / 9,55 = 1500 / 9,55 = 157 ≈ 150 с.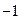

В паспорте электродвигателя указана угловая скорость вала электродвигателя

ω = 314 с.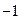

Найти частоту вращения вала этого электродвигателя.

Частота вращения вала

n = 9,55 ω = 9,55*314 = 3000 ≈ 3140 об/ мин.

Угловая скорость. Формула угловой скорости

Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч – значит за один час проехать 100 километров.

А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца – делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!

Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?

Понятие угловой скорости

Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).

Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» – ω.

Классическая формула угловой скорости вращения рассматривается так.

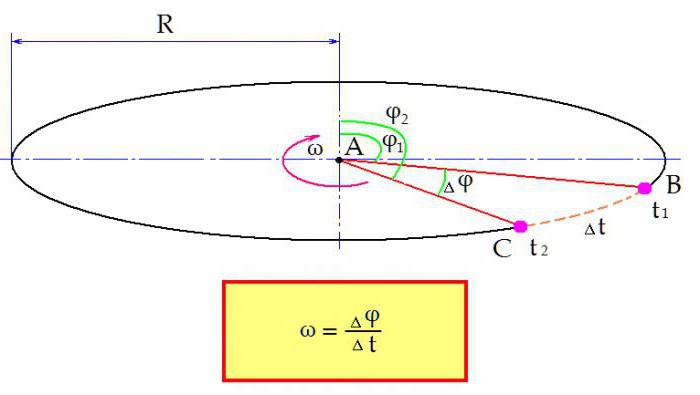
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.

Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:

Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:

Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.

Единицы измерения угловой скорости

Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.

Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.

Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.

Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.

Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.

Период обращения

Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:

Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.

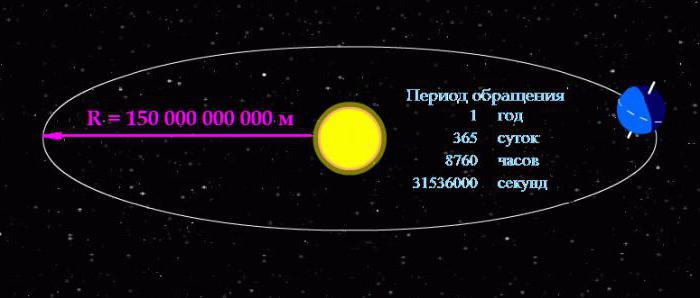
Формула угловой скорости позволяет вычислить её, зная период обращения:

ω = 2П/31536000 = 0,000000199238499086111 рад/с.

Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.

Связь угловой и линейной скоростей

В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.

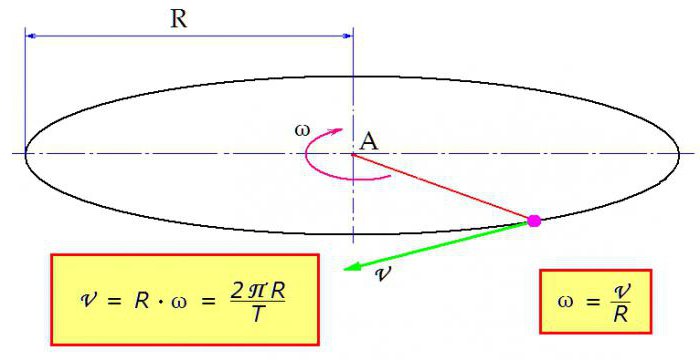
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.

Угловая скорость

градус/с, оборот/с, оборот/мин

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где — радиус-вектор точки (из начала координат), — скорость этой точки. — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

Связь с конечным поворотом в пространстве

• Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве. Тогда угловая скорость, соответствующая этому повороту, равна

.

• Если поворот задан матрицей поворота, где — символ Кронекера, — символ Леви-Чивиты (суммирование ведется по правилу Эйнштейна от 1 до 3), выражение для элементов которой через и могут быть получены, например, с помощью формулы Родрига, то угловая скорость равна

.

• Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .

• В случае, когда поворот описывается с помощью вектора , изменяющегося во времени, обозначим , а также — матрица половинного поворота , — квадрат модуля вектора . Тогда угловая скорость:

.

См. также

Литература

• Лурье А. И. Аналитическая механика\ А. И. Лурье. – М.: ГИФМЛ, 1961. – С. 100-136

Wikimedia Foundation . 2010 .

Смотреть что такое “Угловая скорость” в других словарях:

УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедия

УГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, скорость изменения угловой позиции предмета относительно фиксированной точки. Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2 q1)w)/t. Мгновенной угловой скоростью… … Научно-технический энциклопедический словарь

УГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости w=Dj/Dt, где Dj приращение угла поворота за промежуток времени Dt … Современная энциклопедия

УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости , где приращение угла поворота за промежуток времени ?t … Большой Энциклопедический словарь

угловая скорость — Кинематическая мера вращательного движения тела, выражаемая вектором, равным по модулю отношению элементарного угла поворота тела к элементарному промежутку времени, за который совершается этот поворот, и направленным вдоль мгновенной оси… … Справочник технического переводчика

угловая скорость — векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарь

угловая скорость — kampinis greitis statusas T sritis automatika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Automatikos terminų žodynas

угловая скорость — kampinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, lygus kūno pasisukimo kampo pirmajai išvestinei pagal laiką: ω = dφ/dt; čia dφ – pasisukimo kampo pokytis, dt – laiko tarpas. Kai kūnas sukasi tolygiai … Penkiakalbis aiškinamasis metrologijos terminų žodynas

угловая скорость — kampinis greitis statusas T sritis fizika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynas

Угловая скорость — величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. ω =Δφ/ Δt, где Δφ приращение угла поворота φ за промежуток времени Δt. В общем случае У. с. численно равна… … Большая советская энциклопедия

Теория и решение задач

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

• Количество оборотов за единицу времени [об/мин], [c -1 ].
• Угол поворота за единицу времени [рад/с].

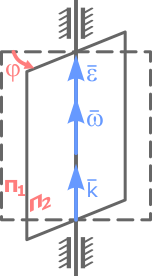
Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

Приняв k как единичный орт положительного направления оси, получим:

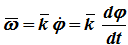
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

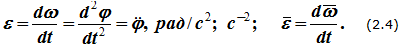
Единицы измерения углового ускорения: [рад/с 2 ], [с -2 ]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

равномерное вращение (ω — const)

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан: