Формула линейной скорости при вращательном движении

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

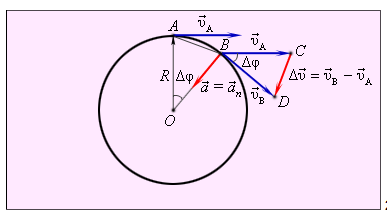
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

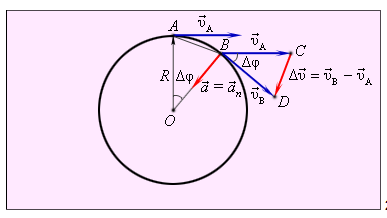
Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Вращательное движение

Круговым движением точки около некоторой оси называется такое движение, при котором траекторией точки является окружность с центром на этой оси, причем плоскость окружности перпендикулярна к этой оси.

Вращательным движением тела вокруг некоторой оси называется такое движения, при котором все точки тела совершают круговое движение вокруг этой оси.

Равномерным вращением называется такое движение, при котором тело за любые равные промежутки времени поворачивается на один и тот же угол.

Угловая скоростьравномерного движения (ω) есть величина, измеряемая углом поворота за единицу времени:

ω = φ / t ,

где φ –угол поворота за время t, измеряемый в радианах (рад).

Угловая скорость может быть выражена через частоту вращения (n) в единицу времени или период обращения Т:

ω = 2π n = (2π /60) n_м= 0,1047 n_м ; ω = 2π /Т.

где n – частота вращения в об/с; n_м -частота вращения в об/мин.

Линейной скоростью точки во вращательном движении называется мгновенная скорость движущейся точки. Она направлена по касательной к траектории. Угловая скоростьωсвязана с линейной скоростью V:

V = ω R,

где R – расстояние от точки до оси вращения.

В случае неравномерного вращательного движения различают мгновенную и среднюю угловые скорости. Если за время от момента t до момента t +Δt тело повернулось на угол Δφ, то средней угловой скоростью (ω_ср) за промежуток времени Δt называется отношение:

Предел этого отношения – это мгновенная угловая скорость:

Вращение, при котором за любые равные промежутки времени угловая скорость изменяется на одну и ту же величину, называется равнопеременным.

Угловым ускорениемравнопеременного вращения ( j ) называется величина, измеряемая изменением угловой скорости в единицу времени:

где ω_t– угловая скорость в момент времени t, а ω – угловая скорость в момент начала отсчета времени.

Если равнопеременное вращательное движение характери зовать частотой вращения (n) в единицу времени, то можно ввести ускорение j*:

где n _t– частота вращения в момент времени t, n – частота вращения в момент начала отсчета времени.

Угловая скорость равнопеременного вращения и частота вращения по истечении времени t после начала вращения равны:

ω = ω + j t, n = n + j* t.

Угол поворота при равнопеременном вращении и частота вращения:

При равнопеременном вращении линейная скорость V любой точки тела меняется и по величине, и по направлению. Изменение величины линейной скорости характеризуется тангенциальным ускорением:

где V_t– скорость в момент времени t , V– скорость в момент начала отсчета времени.

Направление а_т в данной точке траектории совпадает с направлением V. Тангенциальное ускорение а_т связано с угловым ускорением j соотношением:

Однако и при равномерном вращении тела точки тела движутся с ускорением, так как направление их скорости все время меняется. Это ускорение направлено к оси вращения (т.е. перпендикулярно к направлению линейной скорости) и носит название центростремительного ускорения:

где V – линейная скорость, ω –угловая скорость,R – радиус вращения материальной точки.

Полное ускорениеточки тела при равнопеременном вращательном движении:

а = (а_ц 2 + а_т 2 ) 0,5 .

Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики – “Кинематика и динамика вращательного движения”.

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела – это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

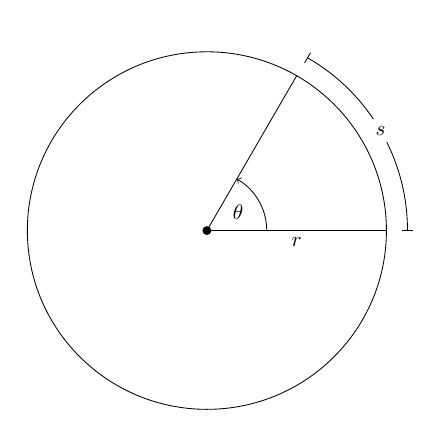
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

Если φ измерять в радианах (1 рад – это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

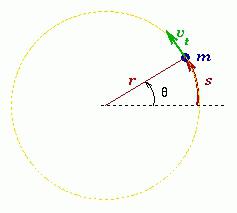
Угловая скорость материальной точки или тела – это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T – физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

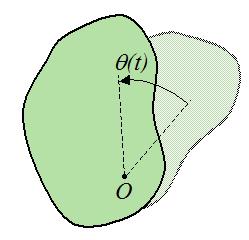
Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено – dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

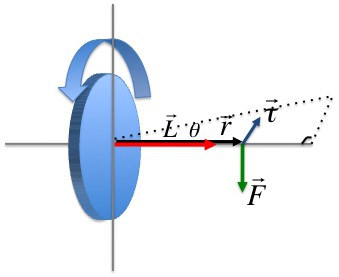
В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I + ma 2 ,

где I – начальный момент инерции тела; m – масса тела; a – расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан – безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота – радиан), получим связь угловой скорости и периода вращения

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7.5) для второй точки получаем

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

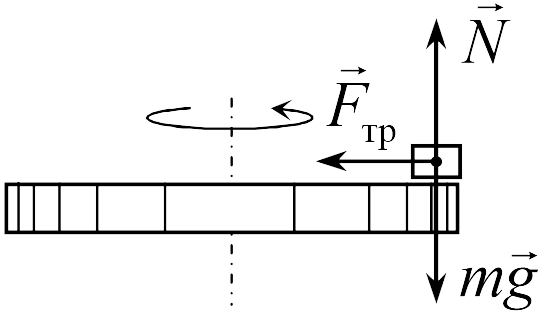
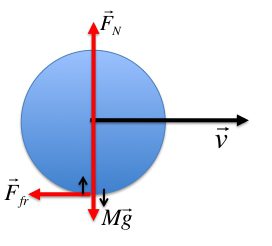
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с 2 , получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим