Скорость столкновения двух автомобилей
Занимательная физика. Что происходит с машинами и водителями при столкновении, и правда ли, что внедорожник “безопаснее” легковушки?
14 июня 2013 в 10:42
TUT.BY
Не секрет, что с безопасностью автомобиля связано множество мифов. В форумах, ЖЖ и офлайновых дискуссиях полно советов на тему того, какой автомобиль безопаснее и как лучше себя вести в аварийной ситуации. Большинство этих советов если не бесполезны, то малоосмысленны – человек советует покупать “пятизвездочный” автомобиль по EuroNCAP, а почему, как, собственно, и что эти звезды значат – объяснить не может. В частности, практически никто не понимает, как “звезды” соотносятся с вероятностью серьезно пострадать в аварии конкретного типа и при конкретной скорости. Понятно, что чем больше звезд – тем лучше, но насколько это “лучше” и где проходит безопасный предел? Пользователь LiveJournal 0serg посчитал, как, на чем и куда безопаснее врезаться, и разбил в пух и прах теорию EuroNCAP-овских “звезд”.
Один из крайне распространенных мифов состоит в том, что очень часто, когда говорят о лобовом ударе автомобилей, скорости этих автомобилей складывают. Вася ехал 60 км/ч, а со встречки на него вылетел Петя на скорости 100 км/ч, удар – ну и сами понимаете, что там на 100+60 = 160 км/ч от машин осталось. Это – грубейшая ошибка. Реальная “эффективная скорость удара” для машин обычно будет равна приблизительно средней арифметической скоростей Васи и Пети – т.е. около 80 км/ч. И именно эта скорость (а не обывательские 160) и приводит к развороченным автомобилям и человеческим жертвам.
“На пальцах” происходящее можно пояснить таким образом: да, при ударе энергия двух автомобилей суммируется – но и поглощают ее тоже два автомобиля, поэтому на каждый автомобиль приходится лишь половина суммарной энергии удара. Корректный расчет происходящего при ударе доступен даже школьнику, хотя и требует определенной смекалки и воображения. Представим себе, что автомобили в момент удара скользят по ровному шоссе без сопротивления (учитывая, что удар происходит за очень короткое время и действующие на машины силы удара гораздо выше сил трения со стороны асфальта – даже при интенсивном торможении это допущение можно считать вполне справедливым). В этом случае движение при ударе будет полностью описываться одной-единственной силой – силой сопротивления сминаемых корпусов металла. Эта сила, по 3-му закону Ньютона, для обеих машин одинакова, но направлена в противоположные стороны.
Мысленно поставим между машинами тонкий, невесомый лист бумаги. Обе силы сопротивления (первой машины и второй) будут действовать “через” этот лист, но поскольку эти силы равны и противонаправленны, то они полностью компенсируют друг друга. А стало быть, на протяжении всего удара наш лист будет двигаться с нулевым ускорением – или, другими словами, с постоянной скоростью. В инерциальной системе координат, связанной с этим листом, обе машины как бы “врезаются” с разных сторон в этот неподвижный лист бумаги – до тех пор, пока не остановятся либо (одновременно) не отлетят от него. Вспоминаете методику EuroNCAP где машины врезаются в неподвижный барьер? Удар о наш гипотетический “лист бумаги” в нашей специальной системе координат будет равносилен удару о массивный бетонный блок на той же скорости.
Как посчитать скорость листа бумаги? Это довольно просто – достаточно вспомнить механику соударений из школьной программы. В какой-то момент оба автомобиля “останавливаются” относительно системы координат листа бумаги (это происходит в то мгновение, когда автомобили начинают разлетаться в разные стороны), что позволяет нам записать закон сохранения импульса. Считая массу одного автомобиля m1 и скорость v1, а другого – m2 и скорость v2, получаем скорость листа бумаги v по формуле
(m1+m2)*v = m1*v1 – m2*v2
v = m1/(m1+m2)*v1 – m2/(m1+m2)*v2
Для столкновения в “попутном” направлении скорость второй машины следует считать со знаком “минус”.
Относительные скорости машин относительно бумаги (т.е. “эквивалентная скорость удара о бетонный блок”) соответственно равны
u1 = (v1-v) = m2/(m1+m2) * (v1+v2)
u2 = (v+v2) = m1/(m1+m2) * (v1+v2)
Таким образом, “эквивалентная скорость” лобового удара действительно пропорциональна сумме скоростей автомобилей – однако берется она с неким “поправочным коэффициентом”, учитывающим соотношение масс автомобилей. Для автомобилей равной массы он равен 0,5, т.е. суммарную скорость нужно поделить пополам – что и дает нам упомянутое в начале заметки типичное для подобных аварий “среднее арифметическое”. В случае столкновения машин разной массы картина будет существенно иной – “тяжелая” машина пострадает меньше, чем “легкая”, причем если различия в массе достаточно велики – разница будет колоссальной. Это типичная ситуация для аварий класса “влетела легковушка в груженый грузовик” – последствия такого удара для легковушки близки к последствиям удара на полноценной “суммарной” скорости, в то время как “грузовик” отделывается небольшими повреждениями, т.к. для него “эквивалентная скорость удара” оказывается равной десятой, а то и двадцатой доле суммарной скорости.
Итак, мы научились считать “эквивалентную скорость удара” по очень простой формуле: нужно сложить скорости (для удара в попутном направлении – вычесть), а затем определить, какую долю массы составляет ЧУЖАЯ машина от суммарной массы ваших машин и умножить этот коэффициент на посчитанную скорость. Прикидочные значения коэффициента:
Машины примерно одинаковой весовой категории: 0.5
Малолитражка vs легковушка: малолитражка 0.6, легковушка 0.4
Малолитражка vs джип: малолитражка 0.75, джип 0.25
Легковушка vs джип: легковушка 0.65, джип 0.35
Легковушка vs грузовик: легковушка >0.9, грузовик 0.8, грузовик
1. Не превышайте сильно скорость. Шансы погибнуть после 120 км/ч растут ОЧЕНЬ быстро, хотя для тяжелых автомобилей безопасный верхний предел обычно несколько выше – увы, за счет безопасности окружающих.
2. Если превышаете – пристегивайтесь. Хотя для относительно небольших скоростей (0-100) без ремня достаточно много шансов выжить, в диапазоне скоростей 100-140 при аварии часто непристегнутые = трупы.
Читать еще: Шкода фабия универсал 2007 года
3. Современный тяжелый автомобиль почти всегда значительно безопаснее в авариях с более легкими автомобилями. К авариям с участием грузовиков или вылетом с трассы данное соображение не относится. Не забывайте только, что большая масса далеко не всегда компенсирует плохую пассивную безопасность – старье 20-летней давности настолько хуже современных 4-5-“звездочных” автомобилей, что его вообще мало что может спасти в аварии.
4. Удар о неподвижное тяжелое препятствие на обочине для тяжелой машины опаснее лобового столкновения. Для легкой машины – наоборот.
5. Удар о неподвижную машину и тем более – машину двигающуюся в попутном направлении всегда гораздо безопаснее удара о неподвижное тяжелое препятствие на обочине.
6. Если вы видите, что сейчас будет авария, а уворачиваться уже поздно – тормозите, как то и предписано ПДД. Пытаться вылететь на обочину, не сбрасывая скорости, обычно как минимум не менее опасно.
7. Исключением из пункта 6 является только тот случай, когда вам в лоб на большой скорости летит грузовик – тут лучше делать что угодно, но с его пути уходить. Но эта ситуация мне в реальной жизни пока не встречалась ни разу (а чтобы самим не вылетать на грузовики на большой скорости – см. пункт 1).
Миф о лобовом столкновении: правду знают только криминалисты
«За рулем» опровергает самую популярную страшилку.
Не дай вам Бог на полном ходу врезаться в дерево или стену. И уж совсем страшные последствия влечет за собой лобовое столкновение: ведь к вашей скорости фактически добавляется скорость встречной машины. А энергия, как учат в школе, пропорциональна квадрату скорости — в общем, о последствиях жутко думать.
Между тем, если все-таки подумать и вспомнить школьную физику, то. получается неожиданный вывод. Складывать скорости вовсе не нужно! И если, к примеру, на трассе сталкиваются лоб в лоб две одинаковые легковушки, двигавшиеся с равными скоростями, то энергия удара для каждой из них будет определяться только ее скоростью и массой. Иными словами, последствия для нее окажутся примерно такими же, как от удара в неподвижную стену! А вовсе не удвоенной и не учетверенной.
Непонятно? Между тем все просто — ситуацию описывал еще Яков Исидорович Перельман в своей «Занимательной механике». Действительно, если предположить, что в момент удара одна из машин стояла на месте, то очевидно, что последствия такой аварии будут куда менее страшными, чем при ударе в массивную неподвижную стену. Два столкнувшихся таким образом автомобиля продолжат движение и будут отброшены довольно далеко от точки столкновения; при этом энергия деформации поделится между ними, грубо говоря, пополам. А вот если тупо вмазаться в стену, то никакой траты энергии на перемещение уже не будет: вся накопленная энергия израсходуется на деформацию одного кузова. Если же теперь предположить, что вторая машина в момент столкновения тоже обладала скоростью, то по мере ее увеличения перемещение скомканных кузовов от точки удара будет сокращаться и, наконец, при равенстве скоростей, машины останутся после аварии в точке удара. При этом последствия такой аварии будут аналогичны удару в стену.
Таким образом, столкновение двух машин равной массы на скорости, к примеру, 100 км/ч будет аналогично удару об стену на тех же 100 км/ч, а вовсе не на 200 км/ч. Примерно об этом и говорил Перельман, описывая знаменитый опыт с магдебургскими полушариями. Напоминаю — их пытались разъединить две упряжки по 8 лошадей, тянувших в противоположные стороны. Но того же эффекта можно было бы добиться, обойдясь всего одной восьмеркой лошадей и прицепив одно из полушарий к неподвижной массивной стене…
Само собой, что если массы автомобилей значительно различаются, то и последствия такого столкновения будут как при контакте слона с Моськой. Во всех случаях тяжеленный «слон» пострадает заведомо меньше, чем крошечная «Моська».
Выводы довольно мрачные, но все-таки озвучу их. Для тяжелого автомобиля лобовуха с легкой машинкой может быть безопаснее наезда на неподвижное препятствие типа стены или опоры моста. Для маленькой машинки подобная «встреча» опаснее. Для машин равной массы разницы нет.
А совет в итоге простой: не гоните лошадей, друзья. Все-таки энергия до сих пор пропорциональна квадрату скорости…
Вот почему при лобовом ударе скорости автомобилей не складываются
Если две машины одновременно движутся на скорости 100 км в час на встречу друг другу и происходит лобовое столкновение, то складываются ли скорости в момент удара?

Среди автолюбителей ходит масса правдоподобных мифов, в которые верит большое количество людей. О многих мифах мы уже не раз писали на страницах нашего издания. Сегодня же мы хотим поговорить о самом распространенном мифе – о складывании скоростей двух автомобилей при лобовом ударе. Давайте развеем этот миф раз и навсегда.
Как-то так повелось, что многие люди считают, что если два автомобиля сталкиваются лоб в лоб, то энергия удара будет соответствовать удвоенной скорости каждого из автомобилей. То есть, как полагают многие автолюбители, чтобы понять, какой силы будет лобовой удар, нужно сложить скорости обоих попавших в ДТП автомобилей.
Чтобы понять, что это миф, и чтобы рассчитать силу лобового удара и последствия для автомобилей, попавших в такую аварию, нужно провести следующее сравнение.

Итак, давайте сравним последствия для автомобилей в разных авариях. Например, каждая машина движется навстречу друг другу со скоростью 100 км/ч, и затем они лоб в лоб сталкиваются друг с другом. Как вы думаете, последствия от лобового удара будут серьезнее, чем от удара в кирпичную стену на той же скорости? Если основываться на распространенном мифе, который уже несколько десятков лет ходит среди людей, только наполовину знающих физику (или вообще не знакомых с ней), то на первый взгляд последствия лобового удара двух автомобилей на скорости 100 км/ч будут более плачевными, чем при ударе автомобиля на той же скорости о кирпичную стену, так как якобы сила лобового удара будет больше из-за того, что скорости машин в этом случае нужно сложить. Но это не так.
Читать еще: Стойки стабилизатора лачетти артикул
На самом деле сила лобового удара двух машин на скорости 100 км/час будет соответствовать той же силе, что и при ударе на скорости в 100 км/час в кирпичную стену. Это можно объяснить двумя способами. Один – простой, который будет понятен даже школьнику. Второй – более сложный, который поймут не все.
ПРОСТОЙ ОТВЕТ
Действительно, полная энергия, которая должна быть рассеяна с помощью смятия металла кузова, вдвое выше при столкновении двух машин лоб в лоб, нежели при ударе одного автомобиля о кирпичную стену. Но при лобовом столкновении увеличивается расстояние смятия металла кузовов обеих машин.
Поскольку изгиб металла – это то место, где идет вся эта кинетическая энергия, то при столкновении двух машин лоб в лоб энергии будет поглощаться в два раза больше, поскольку она будет поглощаться двумя автомобилями, в отличие от удара об кирпичную стену, где кинетическая энергия будет поглощаться одной машиной.
Таким образом, скорость замедления и сила лобового удара на скорости 100 км/час будет примерно той же, что и при ударе на 100 км/час в кирпичную неподвижную стену. Поэтому последствия для двух автомобилей, двигающихся с одинаковой скоростью и столкнувшихся лоб в лоб, будут примерно такими же, как если бы один автомобиль с той же скоростью врезался в неподвижную стену.
БОЛЕЕ СЛОЖНЫЙ ОТВЕТ
Предположим, что автомобили имеют одинаковую массу, одни и те же характеристики деформации и идеально под прямым углом сталкиваются лоб в лоб и не отлетают друг от друга далеко. Допустим, что оба автомобиля остановятся в точке столкновения. Таким образом, двигаясь, например, со скоростью 100 км/час, каждый автомобиль остановится при ударе с 100 до 0 км/час. В этом случае каждый автомобиль будет вести себя точно так же, как если бы каждый из них столкнулся с неподвижной стеной на скорости 100 км/час. В итоге оба автомобиля получат при идеальном лобовом ударе тот же урон, что и при ударе об стену.
Чтобы понять, почему именно одинаковый урон, нужно провести мысленный эксперимент. Для этого представьте, что два автомобиля едут на скорости 100 км/час навстречу друг другу. Но на дороге между ними стоит толстая, очень крепкая неподвижная стена. А теперь представьте, что оба автомобиля одновременно врезаются в эту воображаемую стену с противоположных сторон. Каждый в этот момент одновременно останавливается со 100 км/час до 0 км/час. Поскольку стена на дороге очень прочная, она не передает энергию удара одного автомобиля на другой. В итоге получается, что оба автомобиля ударяются отдельно в стоящую стену, не оказывая влияния друг на друга.
А теперь повторите этот мысленный эксперимент с более тонкой и не очень крепкой стеной, но способной выстоять под ударом. В этом случае, если удар будет одновременно с двух сторон, стена останется стоять на месте. А теперь представьте вместо стены лист прочного куска резины. Поскольку два автомобиля врезаются в него одновременно, лист резины останется стоять на месте, поскольку оба автомобиля будут удерживать резину на одном месте в момент одновременного удара. Но тонкий лист резины не может повлиять на замедление любой машины, поэтому даже если вы уберете лист резины между автомобилями, которые сталкиваются лоб в лоб, каждый автомобиль по-прежнему в момент удара остановится со 100 км/час до 0 км/час, то есть точно так же, как если бы один автомобиль врезался в крепкую неподвижную стену со скоростью 100 км/час.
Одинаковая ли энергия удара и последствия при столкновении со стоящим автомобилем или неподвижной стеной?

Это еще один распространенный миф среди автолюбителей, который связан с тем, что если на скорости, например, в 100 км/час столкнуться со стоящим автомобилем, то сила удара будет точно такой же, как если бы автомобиль на скорости в 100 км/час влетел в неподвижную стену. Но и это не так. Это чистый воды миф, который основан на незнании элементарной физики.
Итак, представим себе ситуацию, что один автомобиль движется со скоростью 100 км/час и на полном ходу сталкивается с точно такой же машиной, стоящей на дороге. В момент удара один автомобиль, продолжая свое движение, будет толкать другой автомобиль. В итоге обе машины отлетят от места столкновения. В момент удара кинетическая энергия будет поглощаться деформацией кузова обоих автомобилей. То есть энергия удара также поделится между двумя автомобилями. В случае же с ударом в неподвижную стену одного автомобиля на скорости в 100 км/час деформация кузова будет только у одного автомобиля. Соответственно, сила удара и его последствия для машины будут больше, чем при ударе на скорости одного автомобиля в другой, который стоит на месте.
При столкновении скорости не складываются.
Я решил написать это пост после прочтения комментария #comment_93066011 и ответов к нему.

В качестве доказательства приводится видео “разрушителей легенд” “суммируется ли скорость при лобовухе?” https://rutube.ru/video/efd5028bdded788fbc800cdb2be8826e/
В видео проводится три эксперимента:
1) Автомобиль на скорости 50 миль в час врезается в бетонную стену.
2) Автомобиль на скорости 100 миль в час врезается в бетонную стену
3) Два автомобиля двигаются друг другу навстречу со скоростью 50 миль в час каждый, автомобили совершают лобовое столкновение.
Читать еще: Трансмиссия что входит в состав

В первом и третьем случае автомобили повреждаются одинаково, а во втором случае автомобиль повреждается очень сильно.
Насколько я понимаю, люди, посмотрев это видео, делают следующий вывод: повреждения автомобиля зависят от его скорости – автомобиль на скорости 50 миль в час получает определенные повреждения, на скорости 100 миль в час бОльшие повреждения. От скорости того, во что он въехал повреждения не зависят.
А может быть другой вывод: повреждения в аварии зависят от максимальной скорости в аварии. Потому, что в первом случае я не знаю, как они объяснили бы повреждения стоящего автомобиля, в который въехал, к примеру, груженый камаз. Ведь скорость такого автомобиля 0 – он не должен был бы получить вообще никаких повреждений.
Но на самом деле этому видео не хватает еще одного эксперимента:
4) Автомобиль на скорости 100 миль в час врезается в стоящий незакрепленный автомобиль.
Если я правильно понял, те, кто считает, что “при лобовом столкновении скорости не складываются”, скажут, что повреждения автомобилей в четвертом эксперименте будут соответствовать второму. Т.е. будут бОльшими, чем при лобовом столкновении на скорости 50 миль в час, т.к. автомобиль двигался с бОльшей скоростью: 100 миль в час. Но, если все посчитать, то получится не так.
Давайте посмотрим, что об этом говорит диванная физика за 7 класс.
Чтобы было проще считать, примем массу автомобиля 1000 кг, массу стенки 99 000 кг (в 7 классе мы еще не умеем в бесконечность), скорости автомобилей 20 и 40 м/с вместо 50 и 100 миль в час соответственно. Столкновения будем считать абсолютно неупругими. Т.е. вся энергия удара пойдет в повреждения автомобилей. После удара автомобили и стенки слипаются, двигаются с одной скоростью.
Скорость после столкновения будем находить из закона сохранения импульса:
m1*V1 + m2*V2 = (m1+m2) V => V = (m1*V1+m2*V2)/(m1+m2)
Напоминаю, что кинетическая энергия вычисляется по формуле (m*V^2)/2
Из закона сохранения энергии следует, что энергия системы до столкновения и после должна быть равна.
До столкновения энергия равна сумме кинетических энергий автомобилей (или стенок).
После – к сумме кинетических добавится энергия деформации. Энергия деформации и будет характеризовать повреждения.
Эксперимент первый с точки зрения неподвижного наблюдателя:
Энергия автомобиля = 0,5*1000*20^2 = 200 кДж.
Энергия стенки = 0. Стенка покоится относительно неподвижного наблюдателя.
Суммарная кинетическая энергия до столкновения 200 кДж.
Скорость после столкновения = (1000*20 + 99000*0) / (1000+99000) = 0,2 м/с
Кинетическая энергия после столкновения = 0,5*100000*0,2^2 = 2 кДж.
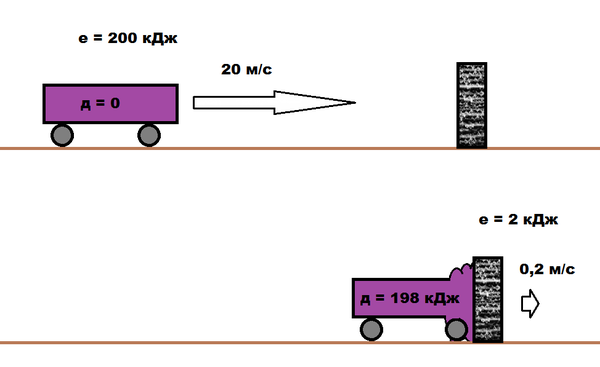
Энергия деформации равна их разности: 198 кДж. Т.к. стенка у нас неразрушимая, то все повреждения получает автомобиль.
Рассмотрим первый эксперимент с точки зрения автомобиля:
Энергия автомобиля = 0, в этой системе отсчета он покоится.
Энергия стенки = 0,5*99000*20^2 = 19800 кДж.
Вот почему я ранее не принял массу стенки бесконечной. У неё была бы бесконечная кинетическая энергия в системе отсчета связанной с автомобилем. И этот пример нельзя было бы рассматривать.
Тут Вы можете сказать, откуда у стенки такая кинетическая энергия?
Но на самом деле это не важно – результат будет тот же.
Скорость лепешки после столкновения будет = (1000*0 + 99000*20) / (1000 + 99000) = 19,8 м/с
Кинетическая энергия после столкновения будет = 0,5*100000*19,8^2 = 19602 кДж.
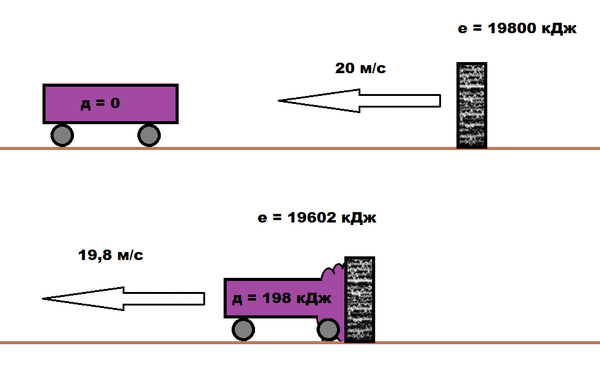
Энергия деформации = 19800 – 19602 = 198 кДж.
Таким образом не важно, в какой системе отсчета мы наблюдаем эксперимент.
Можно рассмотреть относительно центра масс или, например, поезда, проезжающего мимо на скорости 40 м/с. Повреждения будут одинаковыми.
Рассмотрим второй эксперимент только относительно неподвижного наблюдателя:
Энергия автомобиля = 0,5*1000*40^2 = 800 кДж.
Энергия стенки = 0.
Скорость после столкновения = (1000*40 + 99000*0) /(1000+99000) = 0,4 м/с
Кинетическая энергия лепешки = 0,5*100000*0,4^2 = 8 кДж.
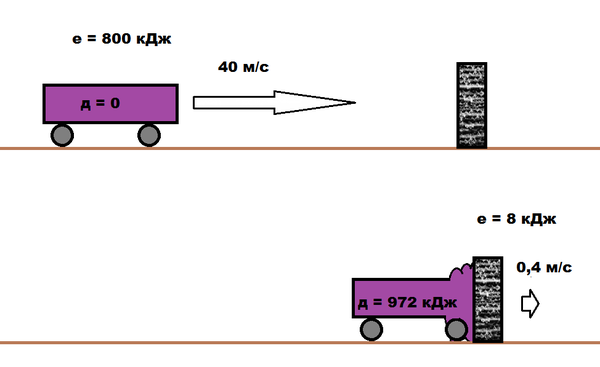
Энергия деформации = 972 кДж.
Пока все сходится. В видео видно, что автомобиль повредился во втором эксперименте значительно сильнее.
Если есть желание, можете сами посмотреть относительно автомобиля. Результат будет тот же.
Третий эксперимент. Относительно земли.
Энергия обоих автомобилей = 0,5*1000*20^2 = 200 кДж.
Суммарная кинетическая энергия до столкновения 400 кДж.
Суммарная кинетическая энергия после столкновения = 0 т.к. лепешка не будет двигаться поле столкновения.
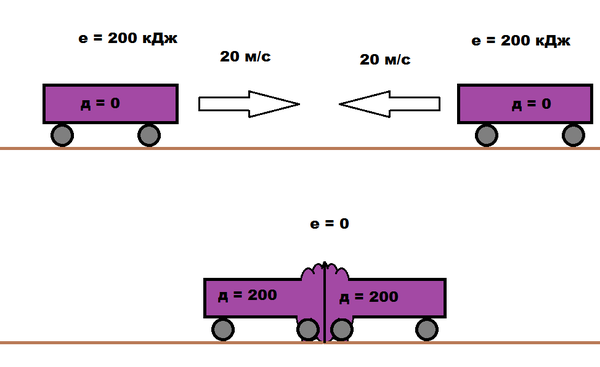
Оба автомобиля повредятся одинаково: каждый на 400/2 = 200 кДж.
Это опять соответствует тому, что мы видели в видео. В первом и третьем эксперименте автомобили повреждаются примерно одинаково.
А теперь рассмотрим третий эксперимент относительно одного из автомобилей.
Это будет в точности соответствовать четвертому эксперименту!
С точки зрения одного из автомобилей он покоится, а другой движется ему навстречу со скоростью 40 м/с. Независимо от того, покоится он на самом деле или движется. На самом деле, дальше можно не считать. Т.к. уже должно стать понятно, что результат третьего эксперимента не изменится, если выбрать другую систему отсчета. Но, чтобы убедиться.
Энергия покоящегося автомобиля = 0
Энергия движущегося = 0,5*1000*40^2 = 800 кДж.
После столкновения лепешка будет двигаться со скоростью = (0*1000 + 40*1000) / (1000+1000) = 20 м/с.
Кинетическая энергия лепешки = 0,5*(1000+1000)*20^2 = 400 кДж.
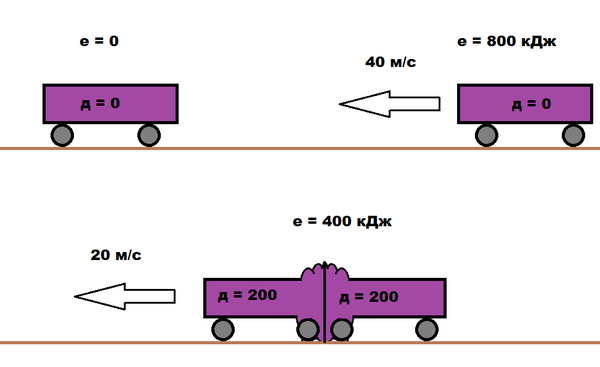
Энергия деформации = 800 кДж – 400 кДж = 400 кДж. Т.о. оба автомобиля “повредятся” на 400 / 2 = 200 кДж.
Когда мы рассматриваем два сталкивающихся автомобиля (а не иногда автомобили, а иногда внезапно неразрушимые сверхтяжелые стенки), то повреждения зависят от суммы их скоростей (скорости сближения). Если автомобили разные, то от их масс и того, как они “принимают” повреждения.
В контексте оригинального поста, если два поезда на скорости в 150 км/ч врезаются лоб в лоб, то это равносильно тому, что один поезд со скоростью 300 км/ч врезается в стоящий поезд.
А в видео “разрушителей легенд” рассмотрен частный случай. Очень неудачный частный случай, из которого сам собой делается неправильный вывод.














