Угловое ускорение блока формула

Теория и решение задач

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

• Количество оборотов за единицу времени [об/мин], [c -1 ].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

Единицы измерения углового ускорения: [рад/с 2 ], [с -2 ]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

равномерное вращение (ω — const)

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Угловая скорость и угловое ускорение

Поворот тела на некоторый угол можно задать в виде отрезка, длина которого равна j, а направление совпадает с осью, вокруг которой производится поворот. Направление поворота и изображающего его отрезка связано правилом правого винта.

При вращательном движении твердого тела каждая точка движется по окружности, центр которой лежит на общей оси вращения (рис. 7). При этом радиус-вектор R, направленный от оси вращения к точке, поворачивается за время Dt на некоторый угол Dj. Для характеристики вращательного движения вводится угловая скорость и угловое ускорение.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Угол в 1 радиан – это центральный угол, длина дуги которого равна радиусу окружности; 360 о = 2p рад.

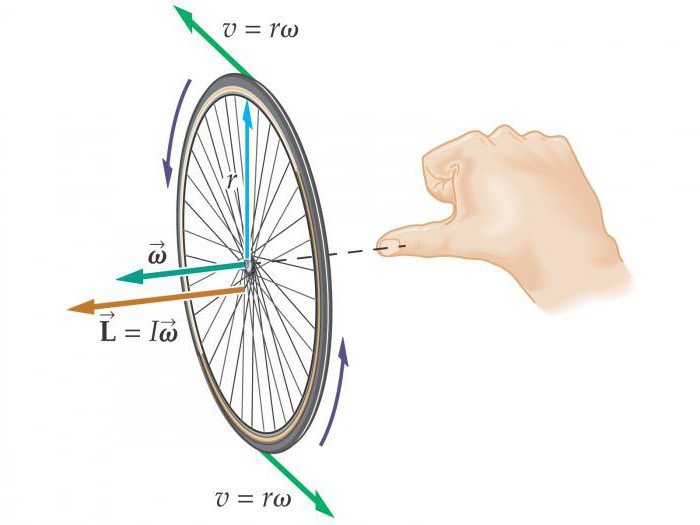
Направление угловой скорости задается правилом правого винта: вектор угловой скорости сонаправлен с , то есть с поступательным движением винта, головка которого вращается в направлении движения точки по окружности.

Линейная скорость точки связана с угловой скоростью:

.

В векторной форме .

Если в процессе вращения угловая скорость изменяется, то возникает угловое ускорение.

Угловое ускорение – векторная величина, равная первой производной угловой скорости по времени:

Вектор угловой скорости сонаправлен с вектором элементарного изменения угловой скорости , происшедшего за время dt.

При ускоренном движении вектор сонаправлен (рис. 8), при замедленном – противонаправлен (рис. 9).

Найдем связь между угловым и тангенциальным ускорениями:

.

Изменение направления скорости при криволинейном движении характеризуется нормальным ускорением :

.

Таким образом, связь между линейными и угловыми величинами выражается следующими формулами:

.

Типы вращательного движения

а) переменное – вращательное движение, при котором изменяются и :

б) равнопеременное – вращательное движение с постоянным угловым ускорением:

.

в) равномерное – вращательное движение с постоянной угловой скоростью:

.

Равномерное вращательное движение можно характеризовать периодом и частотой вращения .

Период – это время, за которое тело совершает один полный оборот.

, [T] = c.

Частота вращения – это число оборотов совершаемых за единицу времени.

, [n] = c -1 .

За один оборот: ,

, .

Угловое ускорение

Угловое ускорение – это псевдовекторная физическая величина, которая равна первой производной от псевдовектора угловой скорости по времени:

.

Угловое ускорение характеризует силу изменения модуля и направления угловой скорости при движении твердого тела.

Ускорение точки твердого тела при свободном движении.

К понятию углового ускорения можно прийти, изучая определение ускорения точки твердого тела, находящегося в свободном движении. Определение скорости точки тела В (по формуле Эйлера) в свободном движении:

.

где – скорость точки тела А, которая была принята как полюс; – псевдовектор угловой скорости тела; – вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:

.

где – является ускорением полюса А; – псевдовектором углового ускорения.

Составляющая ускорения точки В, которая определяется через угловое ускорение называется вращательным ускорением точки В около полюса А.

.

Последнее слагаемое в полученной формуле, которое зависит от угловой скорости, называется осестремительным ускорением точки В вокруг полюса А.

.

Угловое ускорение при вращении тела вокруг неподвижной оси.

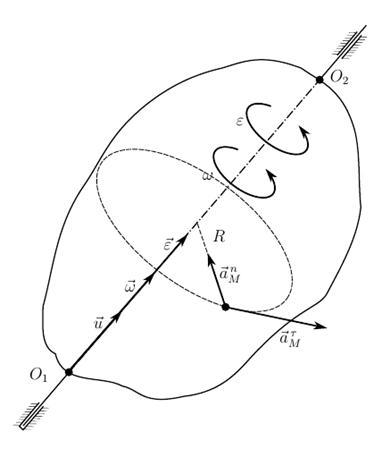
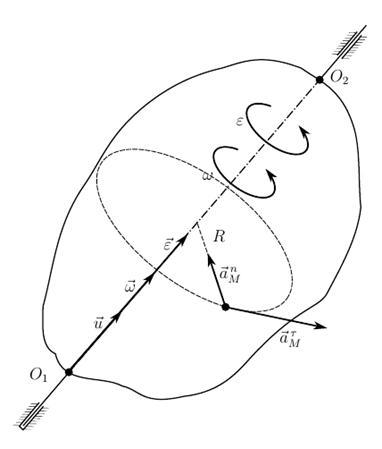
Когда происходит вращение тела около неподвижной оси, которая проходит через недвижимые точки тела О₁ и О₂, производные орта оси вращения = 0:

.

Отсюда вектор углового ускорения вычисляется тривиально через вторую производную угла поворота

или .

где – это алгебраическая величина углового ускорения.

Здесь псевдовектор углового ускорения (и угловая скорость) идет по оси вращения тела. В случае наличия одинакового знака у первой и второй производной угла поворота:

,

значит, вектор углового ускорения и вектор угловой скорости имеют одинаковое направление и тело имеет ускоренное вращение. Иначе, при , векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.

В теормехе обычно вводится понятие угловой скорости и углового ускорения, когда рассматривается вращение тела вокруг не двигающейся оси. При чем, для решения задачи используют зависимость от времени угла поворота тела

Отсюда закон движения точки тела можно выразить натурально, как длина дуги окружности, которую прошла точка, совершая поворот тела от определенного исходного положения φ = φ (t)

где R является расстоянием от точки до оси вращения.

Продифференцировав вышеуказанное выражение по времени, найдем алгебраическую скорость точки:

.

где является алгебраической величиной скорости угловой.

Через геометрическую сумму тангенциального и нормального ускорения можно выразить ускорение точки тела при вращении:

.

При этом тангенциальное ускорение выходит в виде производной от алгебраической скорости точки:

.

где является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:

.

Вращательное движение и угловая скорость твердого тела

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

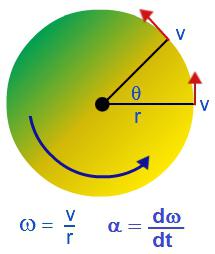
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек – сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной – угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .

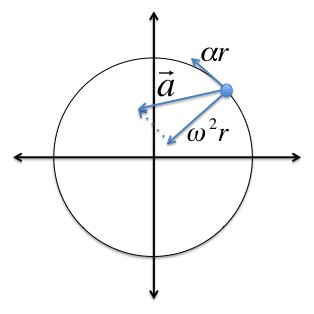
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ + ωt, где φ – начальное значение угла поворота.

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω+ εt, φ = φ + ωt + εt 2 /2.

Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц = v 2 /R = (ωR) 2 /R = ω 2 R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

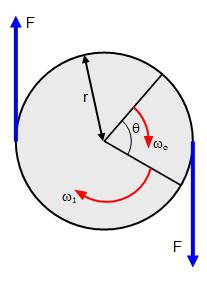
Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α – угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 – момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω – εt.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ + ωt + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ = 0, находим: φ(t)= ωt/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).

Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.

Найдем время, за которое диск остановится: t = ω/ε, где ω – начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.